1. Les ensembles de nombres▲
1-1. Les nombres naturels▲
Les nombres naturels (appelés aussi entiers naturels) sont des nombres qui permettent de compter les entités, par exemple, les doigts, les feuilles d'un arbre. Ils ne permettent pas de mesurer des quantités continues comme une longueur, un volume ou une masse. Au départ, on a par exemple des personnes, des animaux, des objets. Un troupeau est constitué de moutons : dans un troupeau, les moutons sont distincts et à peu près identiques. Leurs caractères communs définissent une collection.
L'idée de considérer zéro comme un entier naturel est relativement récente. Elle correspond au cas où le troupeau ne comporte aucun mouton. L'ensemble des entiers naturels incluant zéro sera noté kitxmlcodeinlinelatexdvp\mathbb{N}finkitxmlcodeinlinelatexdvp . On peut aussi estimer qu'un troupeau qui ne comporte aucun mouton n'est plus un troupeau. C'est pourquoi on définit l'ensemble des entiers naturels excluant zéro qui sera noté kitxmlcodeinlinelatexdvp\mathbb{N}^{*}finkitxmlcodeinlinelatexdvp .
1-1-1. L'addition▲
L'addition est la plus élémentaire des opérations arithmétiques appliquées à deux entiers naturels. Son résultat est la somme : lorsqu'on rassemble deux troupeaux comportant respectivement kitxmlcodeinlinelatexdvpn_1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpn_2finkitxmlcodeinlinelatexdvp moutons, on obtient un troupeau comportant un nombre de moutons égal à la somme kitxmlcodeinlinelatexdvpn_1 + n_2finkitxmlcodeinlinelatexdvp des nombres de moutons des troupeaux initiaux. L'addition est commutative : kitxmlcodeinlinelatexdvpn_1 + n_2 = n_2 + n_1finkitxmlcodeinlinelatexdvp .
Les troupeaux comportent respectivement 107 et 85 moutons. En les rassemblant, on obtient un troupeau de :
kitxmlcodelatexdvp107 + 85 = 85 + 107 = 192\ \mathrm{moutons},finkitxmlcodelatexdvp1-1-2. La soustraction▲
La soustraction est l'opération inverse de l'addition. Son résultat est la différence : lorsqu'un loup égorge un certain nombre de moutons d'un troupeau, le nombre de moutons restants est égal à la différence kitxmlcodeinlinelatexdvpn_1 − n_2finkitxmlcodeinlinelatexdvp entre nombre initial de moutons kitxmlcodeinlinelatexdvpn_1finkitxmlcodeinlinelatexdvp et le nombre de moutons égorgés kitxmlcodeinlinelatexdvpn_2finkitxmlcodeinlinelatexdvp . Comme le loup ne peut pas égorger plus de moutons qu'il n'y en a, le résultat reste nécessairement dans l'ensemble kitxmlcodeinlinelatexdvp\mathbb{N}finkitxmlcodeinlinelatexdvp . La soustraction n'est pas commutative, car on ne peut pas intervertir l'effectif initial du troupeau et le nombre de moutons égorgés.
Le troupeau comporte initialement 192 moutons. Le loup en égorge 9. Il reste :
kitxmlcodelatexdvp192 - 9 = 183\ \mathrm{moutons}.finkitxmlcodelatexdvp1-1-3. La multiplication▲
La multiplication est équivalente à une addition itérée. Son résultat est le produit : si le troupeau a été chargé sur un train, chaque wagon étant supposé complètement rempli, le nombre total de moutons est le produit kitxmlcodeinlinelatexdvpn_1 \times n_2finkitxmlcodeinlinelatexdvp du nombre de wagons kitxmlcodeinlinelatexdvpn_1finkitxmlcodeinlinelatexdvp et du nombre de moutons par wagon kitxmlcodeinlinelatexdvpn_2finkitxmlcodeinlinelatexdvp . La multiplication est commutative.
Un troupeau de moutons est chargé sur un train qui comporte 8 wagons pouvant contenir chacun 24 moutons. Le train peut donc transporter :
kitxmlcodelatexdvp8 \times 24 = 192\ \mathrm{moutons}finkitxmlcodelatexdvpOn pourrait aussi charger ce même troupeau dans 24 remorques pouvant contenir chacune 8 moutons :
kitxmlcodelatexdvp24 \times 8 = 192\ \mathrm{moutons}finkitxmlcodelatexdvp1-1-4. La division▲
La division est l'opération inverse de la multiplication. Son résultat est le quotient : si on prévoit de charger un troupeau sur un train dont chaque wagon peut embarquer un certain nombre de moutons, le nombre de wagons nécessaires sera le quotient kitxmlcodeinlinelatexdvp\dfrac{n_1}{n_2}finkitxmlcodeinlinelatexdvp du nombre total de moutons kitxmlcodeinlinelatexdvpn_1finkitxmlcodeinlinelatexdvp par le nombre de moutons par wagons kitxmlcodeinlinelatexdvpn_2finkitxmlcodeinlinelatexdvp . Une division par zéro est impossible, car on ne peut pas transporter un troupeau dans un train dont chaque wagon ne peut contenir aucun mouton.
On veut charger un troupeau de 192 moutons sur un train composé de wagons pouvant contenir chacun 24 moutons. On doit donc prévoir :
kitxmlcodelatexdvp\dfrac{192}{28} = 8\ \mathrm{Wagons}.finkitxmlcodelatexdvpD'autre part, il peut arriver que la division ne puisse pas se faire exactement. Dans ce cas, le dernier wagon sera incomplètement rempli. Il subsiste donc un reste.
Comme le loup a égorgé 9 moutons, il n'en subsiste plus que 183. On aura donc 7 (le quotient) wagons contenant 24 moutons et un qui n'en contiendra que 15 (le reste) :
kitxmlcodelatexdvp183 \ \mathrm{moutons }= 7 \times 24 + 15finkitxmlcodelatexdvpNotons enfin que la division n'est pas commutative : diviser le nombre de wagons par le nombre de moutons n'aurait aucun sens.
1-2. Représentation des nombres naturels▲
Les chiffres sont des caractères typographiques utilisés pour représenter les nombres. Pour la plupart des usages toutefois, on est amené à définir des quantités d'information plus importantes, regroupant plusieurs chiffres.
Diverses collections de chiffres sont utilisées :
1-2-1. Notation binaire▲
Il y a deux chiffres différents :
- 0 : zéro ;
- 1 : un.
La plus petite quantité d'information est le bit, qui est représenté par un 0 ou un 1. En pratique, le bit est optimal pour représenter des grandeurs que l'on appelle binaires, logiques ou booléennes, c'est-à-dire qui ne peuvent prendre que deux valeurs : oui ou non, vrai ou faux, allumé ou éteint, enclenché ou déclenché, etc.
Ainsi, le nombre 951 peut être décomposé en une somme de puissances de 2 :
kitxmlcodelatexdvp\begin{align}951 &= 1 \times 512 + 1 \times 256 + 1 \times 128 + 0 \times 64 + 1 \times 32 + 1 \times 16 + 0 \times 8 + 1 \times 4 + 1 \times 2 + 1 \times 1\\ 951 &= 1 \times 2^9 + 1 \times 2^8 + 1 \times 2^7 + 0 \times 2^6 + 1 \times 2^5 + 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0\end{align}finkitxmlcodelatexdvpIl sera donc noté kitxmlcodeinlinelatexdvp1110110111finkitxmlcodeinlinelatexdvp .
1-2-2. Notation octale▲
Il y a huit chiffres différents :
- 0 : zéro ;
- 1 : un ;
- 2 : deux ;
- 3 : trois ;
- 4 : quatre ;
- 5 : cinq ;
- 6 : six ;
- 7 : sept.
Ainsi, le nombre 951 peut être décomposé en une somme de puissances de 8 :
kitxmlcodelatexdvp\begin{align}951 & = 1 \times 512 + 6 \times 64 + 6 \times 8 + 7 \times 1\\ 951 & = 1 \times 8^3 + 6 \times 8^2 + 6 \times 8^1 + 7 \times 8^0\end{align}finkitxmlcodelatexdvpIl sera donc noté kitxmlcodeinlinelatexdvp1667finkitxmlcodeinlinelatexdvp .
1-2-3. Notation décimale▲
Il y a dix chiffres différents :
- 0 : zéro ;
- 1 : un ;
- 2 : deux ;
- 3 : trois ;
- 4 : quatre ;
- 5 : cinq ;
- 6 : six ;
- 7 : sept ;
- 8 : huit ;
- 9 : neuf.
Ainsi, le nombre 951 peut être décomposé en une somme de puissances de 10 :
kitxmlcodelatexdvp\begin{align}951 &= 9 \times 100 + 5 \times 10 + 1 \times 1\\ 951 & = 9 \times 10^2 + 5 \times 10^1 + 1 \times 10^0\end{align}finkitxmlcodelatexdvpIl sera donc noté kitxmlcodeinlinelatexdvp951finkitxmlcodeinlinelatexdvp .
1-2-4. Notation hexadécimale▲
Il y a seize chiffres différents :
- 0 : zéro ;
- 1 : un ;
- 2 : deux ;
- 3 : trois ;
- 4 : quatre ;
- 5 : cinq ;
- 6 : six ;
- 7 : sept ;
- 8 : huit ;
- 9 : neuf ;
- A : dix ;
- B : onze ;
- C : douze ;
- D : treize ;
- E : quatorze ;
- F : quinze.
Ainsi, le nombre 951 peut être décomposé en une somme de puissances de 16 :
kitxmlcodelatexdvp\begin{align}951 & = 3 \times 256 + 11 \times 16 + 7 \times 1\\ 951 &= 3 \times 16^2 + 11 \times 16^1 + 7 \times 16^0 \end{align}finkitxmlcodelatexdvpIl sera donc noté kitxmlcodeinlinelatexdvp3B7finkitxmlcodeinlinelatexdvp .
1-3. Les nombres entiers relatifs▲
Si on s'intéresse à la variation annuelle de l'effectif de notre troupeau, celle-ci sera égale, chaque année, à la différence kitxmlcodeinlinelatexdvpn_+ − n_−finkitxmlcodeinlinelatexdvp entre le nouveau nombre de moutons kitxmlcodeinlinelatexdvpn_+finkitxmlcodeinlinelatexdvp et l'ancien kitxmlcodeinlinelatexdvpn_−finkitxmlcodeinlinelatexdvp . Si, d'une année à la suivante, l'effectif du troupeau a augmenté, la différence reste dans l'ensemble kitxmlcodeinlinelatexdvp\mathbb{N}finkitxmlcodeinlinelatexdvp . En revanche, si le loup a été particulièrement actif, l'effectif a diminué et la différence n'appartient plus à l'ensemble kitxmlcodeinlinelatexdvp\mathbb{N}finkitxmlcodeinlinelatexdvp .
L'ensemble des nombres entiers relatifs est formé des entiers naturels kitxmlcodeinlinelatexdvp(0, 1, 2, 3\dots)finkitxmlcodeinlinelatexdvp dits entiers relatifs positifs et de leurs opposés kitxmlcodeinlinelatexdvp(0, −1, −2, −3\dots)finkitxmlcodeinlinelatexdvp appelés entiers relatifs négatifs. Il se note kitxmlcodeinlinelatexdvp\mathbb{Z}finkitxmlcodeinlinelatexdvp .
Dans un entier relatif, on distingue son signe (+ ou − ) et sa valeur absolue : l'entier relatif −3 a pour valeur absolue 3.
On a relevé l'effectif du troupeau au début de plusieurs années consécutives :
- 2001 : 174 ;
- 2002 : 186 ;
- 2003 : 178 ;
- 2004 : 188.
Les variations annuelles d'effectif sont donc :
- durant l'année 2001 : kitxmlcodeinlinelatexdvp186 − 174 = 12finkitxmlcodeinlinelatexdvp ;
- durant l'année 2002 : kitxmlcodeinlinelatexdvp178 − 186 = −8finkitxmlcodeinlinelatexdvp ;
- durant l'année 2003 : kitxmlcodeinlinelatexdvp188 − 178 = 10finkitxmlcodeinlinelatexdvp .
L'addition est la plus élémentaire des opérations arithmétiques appliquées à deux entiers relatifs. Son résultat est la somme.
Lorsque les deux entiers relatifs sont de même signe, elle s'obtient en additionnant les deux valeurs absolue et en conservant le signe commun.
kitxmlcodelatexdvp\begin{align}7 + 4 &= 11\\ (-7) + (-4)& = -11\end{align}finkitxmlcodelatexdvpLorsque les deux entiers relatifs sont de signes opposés, elle s'obtient en soustrayant la plus petite des deux valeurs absolues de la plus grande, puis en affectant du signe de l'entier ayant la plus grande valeur absolue.
kitxmlcodelatexdvp\begin{align}7 + (-4) &= 3\\ (-7) + 4 &= -3\end{align}finkitxmlcodelatexdvpLa soustraction est l'opération inverse de l'addition. Son résultat est la différence. Elle est égale à la somme du premier nombre et de l'opposé du second.
kitxmlcodelatexdvp\begin{align}7 - 4 &= 3\\ 7 - (-4) &= 11\\ (-7) - 4 &= -11\\ (-7) - (-4) &= -3\end{align}finkitxmlcodelatexdvpLa multiplication est équivalente à une addition itérée. Son résultat est le produit. Sa valeur absolue est égale au produit des valeurs absolues des deux arguments. Son signe est + si les deux arguments sont de même signe et − s'ils sont de signes opposés.
kitxmlcodelatexdvp\begin{align}7 \times 4 &= 28\\ (-7) \times (-4) &= 28\\ 7 \times (-4) &= -28\\ (-7) \times 4 &= -28\end{align}finkitxmlcodelatexdvpLa division est l'opération inverse de la multiplication. Son résultat est le quotient. Sa valeur absolue est égale au quotient des valeurs absolues des deux arguments. Son signe est + si les deux arguments sont de même signe et − s'ils sont de signes opposés.
kitxmlcodelatexdvp\begin{align}28 / 4 &= 7\\ (-28) / (-4) &= 7\\ 28 / (-4) &= -7\\ (-28) / 4 &= -7\end{align}finkitxmlcodelatexdvpUne division par zéro est impossible. D'autre part, il peut arriver que le quotient n'appartienne plus à l'ensemble kitxmlcodeinlinelatexdvp\mathbb{Z}finkitxmlcodeinlinelatexdvp .
1-4. Les nombres rationnels▲
Un nombre rationnel est un nombre qui peut être exprimé par le quotient de deux entiers relatifs, éléments de kitxmlcodeinlinelatexdvp\mathbb{Z}finkitxmlcodeinlinelatexdvp , dont le second est non nul. L'ensemble des nombres rationnels est noté kitxmlcodeinlinelatexdvp\mathbb{Q}finkitxmlcodeinlinelatexdvp .
Un nombre rationnel peut être exprimé par une fraction, par la somme d'un entier et d'une fraction dont le dénominateur est supérieur au numérateur ou à l'aide de chiffres placés à gauche et à droite d'une virgule (ou un point dans la littérature anglo-saxonne).
kitxmlcodelatexdvp\frac{11}{4} = 2 \frac{3}{4}finkitxmlcodelatexdvpQuelle que soit la base choisie (notation décimale, binaire, etc.), la séquence des chiffres placés à droite de la virgule devient toujours périodique lorsqu'on s'éloigne suffisamment de celle-ci.
Cas échéant, on indique la période en la surmontant d'un trait horizontal.
kitxmlcodelatexdvp\begin{align}\frac{3}{2} &= 1\frac{1}{2} = 1,5\\ \frac{5}{3} &= 1\frac{2}{3} = 1,\overline{6}\\ \frac{7}{4} &= 1\frac{3}{4} = 1,75\\ \frac{9}{5} &= 1\frac{4}{5} = 1,8\\ \frac{11}{6} &= 1\frac{5}{6} = 1,8\overline{3}\\ \frac{13}{7} &= 1\frac{6}{7} = 1,\overline{857142}\end{align}finkitxmlcodelatexdvp1-5. Les nombres réels▲
Un nombre irrationnel est un nombre qui ne peut pas être exprimé par le quotient de deux entiers relatifs. En conséquence, il ne peut pas être écrit avec un nombre fini de chiffres à droite de la virgule. Il existe deux types de nombres irrationnels :
- les nombres algébriques racines d'un polynôme à coefficients rationnels non nuls, comme la racine carrée de 2, et plus généralement tout nombre kitxmlcodeinlinelatexdvp\sqrt{x}finkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp est un nombre rationnel positif qui n'est pas un carré parfait ;
- les nombres transcendants comme kitxmlcodeinlinelatexdvp\pifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpefinkitxmlcodeinlinelatexdvp .
La réunion de l'ensemble des nombres rationnels et de celui des nombres irrationnels forme l'ensemble des nombres réels noté kitxmlcodeinlinelatexdvp\mathbb{R}.finkitxmlcodeinlinelatexdvp
En ajoutant de plus en plus de chiffres après la virgule, il est possible de construire une suite de nombres rationnels qui tend indéfiniment vers un nombre réel donné, mais sans jamais l'atteindre. La recherche d'un nombre rationnel aussi proche que possible est un problème très ancien : le numéro 7289 de la Yale Babylonian Collection ou YBC 7289 est une tablette d'argile babylonienne, écrite en cunéiforme et datée du premier tiers du IIè millénaire av. J.-C. (env. −1700). On ne connaît pas son origine exacte ; elle provient sans doute du sud de l'Irak actuel. Elle est actuellement conservée à l'Université de Yale. Son intérêt réside dans le fait qu'elle est la plus ancienne représentation connue de la racine carrée de deux, notée kitxmlcodeinlinelatexdvp\sqrt2 .finkitxmlcodeinlinelatexdvp
Cette tablette a la forme d'un disque d'environ 8 cm de diamètre et 8 mm d'épaisseur. Sa forme et ses dimensions laissent supposer qu'elle a été utilisée par un apprenti scribe pour résoudre un exercice.
Une face représente un carré et ses diagonales. À l'intérieur, le long d'une diagonale, se trouvent deux séries de chiffres.

La suite 1 ; 24 ; 51 ; 10 peut-être interprétée comme :
kitxmlcodelatexdvp1+\frac{24}{60}+\frac{51}{60^2}+\frac{10}{60^3} = \frac{30547}{21600} = 1,41421\overline{247}finkitxmlcodelatexdvpce qui est très proche de :
kitxmlcodelatexdvp\sqrt{2}\approx 1,414213562finkitxmlcodelatexdvpLa suite 42 ; 25 ; 35 représente l'inverse de la précédente ; elle peut-être interprétée comme :
kitxmlcodelatexdvp\frac{42}{60}+\frac{25}{60^2}+\frac{35}{60^3}=\frac{30547}{43200} \approx 0,707106\overline{481}finkitxmlcodelatexdvpce qui est très proche de :
kitxmlcodelatexdvp\sqrt{1/2}\approx 0,7071067812finkitxmlcodelatexdvpSur un côté de ce carré, on peut lire le chiffre ![]() qui signifie 30 dans le système hexadécimal babylonien. Ce système ne permet pas de connaître la valeur exacte d'un nombre, mais seulement celle-ci à une puissance de 60 près. Ainsi 30 peut-il signifier
kitxmlcodeinlinelatexdvp30finkitxmlcodeinlinelatexdvp
comme
kitxmlcodeinlinelatexdvp30 \times 60finkitxmlcodeinlinelatexdvp
,
kitxmlcodeinlinelatexdvp30 \times 60^2finkitxmlcodeinlinelatexdvp
ou
kitxmlcodeinlinelatexdvp30/60finkitxmlcodeinlinelatexdvp
, etc. Une hypothèse est que le 30 qui apparaît sur le côté du carré signifie :
qui signifie 30 dans le système hexadécimal babylonien. Ce système ne permet pas de connaître la valeur exacte d'un nombre, mais seulement celle-ci à une puissance de 60 près. Ainsi 30 peut-il signifier
kitxmlcodeinlinelatexdvp30finkitxmlcodeinlinelatexdvp
comme
kitxmlcodeinlinelatexdvp30 \times 60finkitxmlcodeinlinelatexdvp
,
kitxmlcodeinlinelatexdvp30 \times 60^2finkitxmlcodeinlinelatexdvp
ou
kitxmlcodeinlinelatexdvp30/60finkitxmlcodeinlinelatexdvp
, etc. Une hypothèse est que le 30 qui apparaît sur le côté du carré signifie :
c'est-à-dire le quotient des deux valeurs précédentes.
1-6. Notations en virgule flottante▲
Les nombres réels sont souvent représentés par deux groupes de chiffres, l'un à gauche et l'autre à droite de la virgule. Cette manière n'est pas toujours commode lorsqu'il s'agit d'écrire des nombres très grands ou très petits. C'est pourquoi on recourt volontiers à l'artifice de la virgule flottante : on divise le nombre par une puissance de 10 pour amener la virgule à proximité des chiffres significatifs et on le multiplie par la même puissance de 10 pour le ramener à sa valeur initiale.
1-6-1. Notation « scientifique » normalisée▲
On divise le nombre par la puissance de 10 qui amène la virgule immédiatement à la gauche des chiffres significatifs et on le multiplie par la même puissance de 10 pour le ramener à sa valeur initiale :
kitxmlcodelatexdvp\begin{align}135000&=0,135 \times 10^6\\ 0,0002461&=0,2461 \times 10^{-3}\end{align}finkitxmlcodelatexdvp1-6-2. Notation « scientifique » non normalisée▲
On divise le nombre par une puissance quelconque de 10 qui déplace la virgule d'un certain nombre de positions et on le multiplie par la même puissance de 10 pour le ramener à sa valeur initiale :
kitxmlcodelatexdvp\begin{align}135200&=13,52 \times 10^4\\ 0,0002461&=0,02461 \times 10^{-2}\end{align}finkitxmlcodelatexdvp1-6-3. Notation « ingénieur »▲
On divise le nombre par la puissance de 1000 qui amène la virgule immédiatement à la droite d'un premier groupe d'un, deux ou trois chiffres significatifs et on le multiplie par la même puissance de 1000 pour le ramener à sa valeur initiale :
kitxmlcodelatexdvp\begin{align} 135200&=135,2 \times 10^3\\ 0,0002461&=246,1 \times 10^{-6} \end{align}finkitxmlcodelatexdvp1-7. Les nombres complexes▲
Comme les ensembles de nombres dont on dispose (naturels, entiers relatifs, rationnels, réels) ne permettent pas de faire tout ce que l'on veut (ou doit), il faut en inventer d'autres.
Considérons les puissances successives du nombre −1 :
kitxmlcodelatexdvp\begin{align} (-1)^0&=1\\ (-1)^1&=-1\\ (-1)^2&=1\\ (-1)^3&=-1 \end{align}finkitxmlcodelatexdvpElles sont représentées sur ce qu'on appelle l'axe réel.

Que se passe-t-il si l'exposant n'est pas un nombre entier, mais n'importe quel nombre réel ? On doit imaginer quel est le chemin que parcourt kitxmlcodeinlinelatexdvp−1xfinkitxmlcodeinlinelatexdvp lorsque kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp passe d'un entier au suivant. Considérons donc la suite kitxmlcodeinlinelatexdvp(−1)^0, (−1)^{1/6}, (−1)^{1/3}, (−1)^{1/2}, (−1)^{2/3}, (−1)^{5/6}, (−1)^1, (−1)^{7/6}finkitxmlcodeinlinelatexdvp . Les points correspondants naviguent entre 1 et -1. Mais, par où passent-ils ? On a décidé arbitrairement de placer leurs positions successives sur un cercle de rayon égal à 1 et centré à l'origine.
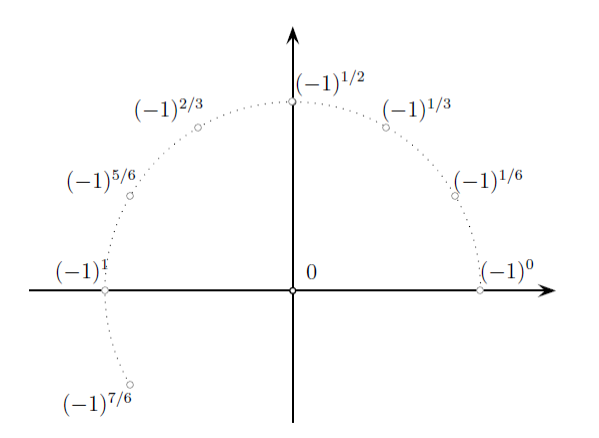
Si (−1) était remplacé par une valeur plus négative, par exemple (−2), le cercle serait remplacé par une spirale logarithmique croissante.
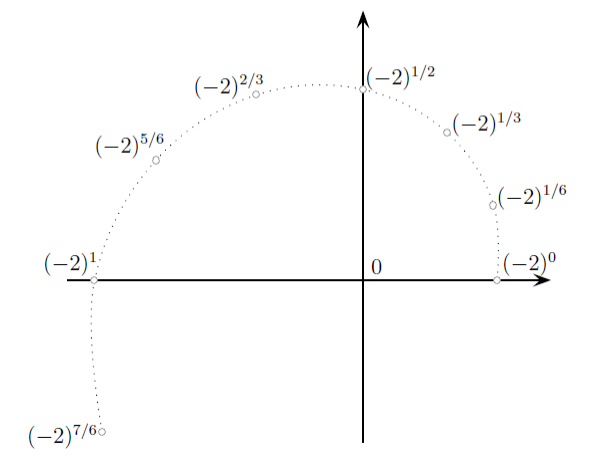
En revanche, si (−1) était remplacé par une valeur moins négative, par exemple (−0,5), le cercle serait remplacé par une spirale logarithmique décroissante.
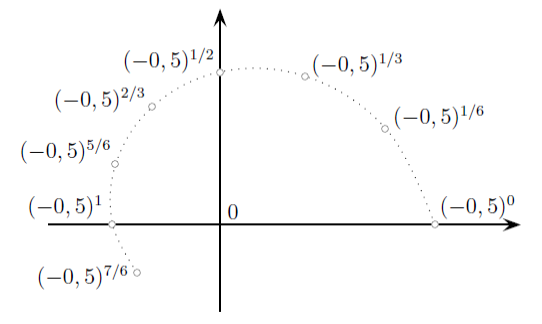
Les diverses valeurs dont la représentation graphique se fait par des points qui ne se trouvent plus seulement sur l'axe réel sont appelées nombres complexes. Le plan sur lequel elles sont représentées est appelé le plan complexe. En plus de l'axe réel, on a un second axe appelé axe imaginaire, sur lequel se trouve le point correspondant à kitxmlcodeinlinelatexdvp(−1)^{1/2}finkitxmlcodeinlinelatexdvp .
Pour indiquer qu'un nombre est complexe, on utilise comme symbole une lettre soulignée, par exemple kitxmlcodeinlinelatexdvp\underline{z}finkitxmlcodeinlinelatexdvp . La position du point représentant le nombre complexe kitxmlcodeinlinelatexdvp\underline{z}finkitxmlcodeinlinelatexdvp peut être exprimée de deux manières, à savoir en coordonnées polaires ou en coordonnées cartésiennes.
- Coordonnées polaires : La distance entre le point 0 (origine) et le point représentant le nombre complexe kitxmlcodeinlinelatexdvp\underline{z}finkitxmlcodeinlinelatexdvp est appelée module ; elle est notée z, |z| ou kitxmlcodeinlinelatexdvp\mod \underline{z}finkitxmlcodeinlinelatexdvp . L'angle entre l'axe réel et la droite qui relie le point 0 et le point représentant le nombre complexe kitxmlcodeinlinelatexdvp\underline{z}finkitxmlcodeinlinelatexdvp est appelé argument ; il est noté kitxmlcodeinlinelatexdvp\arg\underline{z}finkitxmlcodeinlinelatexdvp .
- Coordonnées cartésiennes : la distance entre le point 0 et la projection du point représentant le nombre complexe kitxmlcodeinlinelatexdvp\underline{z}finkitxmlcodeinlinelatexdvp sur l'axe réel est appelée partie réelle de kitxmlcodeinlinelatexdvp\underline{z}finkitxmlcodeinlinelatexdvp : elle est notée kitxmlcodeinlinelatexdvp\operatorname{Re} \underline{z}finkitxmlcodeinlinelatexdvp . La distance entre le point 0 et la projection du point représentant le nombre complexe kitxmlcodeinlinelatexdvp\underline{z}finkitxmlcodeinlinelatexdvp sur l'axe imaginaire est appelée partie imaginaire de kitxmlcodeinlinelatexdvp\underline{z}finkitxmlcodeinlinelatexdvp : elle est notée kitxmlcodeinlinelatexdvp\operatorname{Im} \underline{z}finkitxmlcodeinlinelatexdvp .
Pour simplifier l'écriture, on a tout d'abord appelé kitxmlcodeinlinelatexdvp\mathrm{i}finkitxmlcodeinlinelatexdvp l'unité sur l'axe imaginaire, 1 étant l'unité sur l'axe réel. Par la suite, dans le domaine de l'électrotechnique, on a préféré utiliser la lettre kitxmlcodeinlinelatexdvp\mathrm{j}finkitxmlcodeinlinelatexdvp pour éviter toute confusion avec le symbole du courant. Ainsi, si on a défini :
kitxmlcodelatexdvpx=\operatorname{Re} \ \underline{z}\\ y=\operatorname{Im} \ \underline{z}finkitxmlcodelatexdvpalors un nombre complexe peut s'écrire kitxmlcodeinlinelatexdvp\underline{z}=x+\mathrm{j}yfinkitxmlcodeinlinelatexdvp

Les deux types de coordonnées sont liés par les relations :
kitxmlcodelatexdvpx=z\cos \varphi\\ y=z\sin \varphifinkitxmlcodelatexdvpet, en sens inverse :
kitxmlcodelatexdvpz=|\overline{z}|=\sqrt{x^2+y^2}\\ \tan \varphi = \frac{y}{x}finkitxmlcodelatexdvp2. Le stockage des nombres▲
2-1. Stockage des nombres naturels▲
Le contenu d'un octet peut prendre 256 = 28 valeurs différentes. L'étendue d'une variable stockée sur un octet est l'ensemble des valeurs qu'elle peut prendre. Pour un nombre naturel stocké sur un octet, c'est un sous-ensemble de l'ensemble des nombres naturels kitxmlcodeinlinelatexdvp\mathbb{N}finkitxmlcodeinlinelatexdvp , à savoir l'intervalle fermé kitxmlcodeinlinelatexdvp[ 0 ; 255 ]finkitxmlcodeinlinelatexdvp .
On peut grouper plusieurs octets pour stocker des variables ayant une plus grande étendue.
Le processeur Intel Pentium peut traiter des nombres naturels stockés sur 1, 2, 4 et 8 octets (tableau 2.1). Le C définit les mêmes types de nombres naturels sous d'autres noms. Le Fortran n'offre pas de types de variables spécifiques pour les nombres naturels.
|
Pentium |
C |
Octets |
Bits |
Borne |
|---|---|---|---|---|
|
byte unsigned integer |
unsigned char |
1 |
8 |
28 − 1 |
|
word unsigned integer |
unsigned short |
2 |
16 |
216 − 1 |
|
unsigned int |
||||
|
doubleword unsigned integer |
unsigned long |
4 |
32 |
232 − 1 |
|
quadword unsigned integer |
unsigned long long |
8 |
64 |
264 − 1 |
Table 2.1 - Types de nombres naturels dans le processeur Intel Pentium et en C
2-2. Stockage des nombres entiers relatifs▲
Pour le calcul numérique, on utilise plus souvent des entiers signés, dont l'étendue est un sous-ensemble de l'ensemble des nombres entiers kitxmlcodeinlinelatexdvp\mathbb{Z}finkitxmlcodeinlinelatexdvp . Dans un octet qui contient un nombre entier signé, le premier bit est utilisé pour le signe. S'il vaut 0, le nombre est positif et sa valeur est contenue dans les 7 autres. S'il vaut 1, le nombre est négatif et les 7 autres contiennent sa valeur augmentée de 128 (tableau 2.2).

Le processeur Intel Pentium peut traiter des nombres entiers relatifs stockés sur 1, 2, 4 et 8 octets (tableau 2.3). Le C et le Fortran définissent les mêmes types de nombres naturels sous d'autres noms.
|
Pentium |
C |
Fortran |
Octets |
Bits |
Borne |
|---|---|---|---|---|---|
|
byte signed integer |
char |
Integer*1 |
1 |
8 |
±(27 − 1) |
|
word signed integer |
short |
Integer*2 |
2 |
16 |
±(216 − 1) |
|
int |
|||||
|
doubleword signed integer |
long |
Integer*4 |
4 |
32 |
±(231 − 1) |
|
quadword signed integer |
long long |
Integer*8 |
8 |
64 |
±(263 − 1) |
Table 2.3 - Types de nombres naturels dans le processeur Intel Pentium, en C et en Fortran
Ici se pose la question de l'ordre dans lequel ces octets sont rangés en mémoire. Deux possibilités peuvent être envisagées.
-
Dans le système petit à la fin (en anglais : little endian), l'adresse du mot correspond à l'adresse de l'octet qui contient le signe et les bits les plus significatifs. Les bits les moins significatifs sont stockés dans les octets suivants (tableau 2.4).

Table 2.4 - Entier sur 2 octets, petit à la fin - Dans le système grand à la fin (en anglais : big endian), l'adresse du mot correspond à l'adresse de l'octet qui contient les bits les moins significatifs. Le signe et les bits les plus significatifs sont stockés dans les octets suivants (tableau 2.5).

Il n'est pas nécessaire de prendre garde à cette différence tant qu'on ne travaille que sur un seul type d'ordinateur. En revanche, si l'on veut transférer des données d'un type d'ordinateur à un autre, par exemple d'un ordinateur personnel à un superordinateur ou vice-versa, il faudra peut-être réordonner les octets.
2-3. Stockage des nombres réels▲
Les nombres réels sont des nombres qui peuvent comporter une virgule. Ils sont utilisés pour tout ce qui se mesure, par opposition à ce qui se compte. Dans les ordinateurs personnels, ils sont stockés sur 4, 8 ou 10 octets (32, 64 ou 80 bits). En Fortran, les deux premiers types sont déclarés respectivement comme Real*4 et Real*8. Le stockage sur 80 bits n'est utilisé que dans les registres internes du processeur.
Les nombres sont stockés en virgule flottante, c'est-à-dire sous la forme :
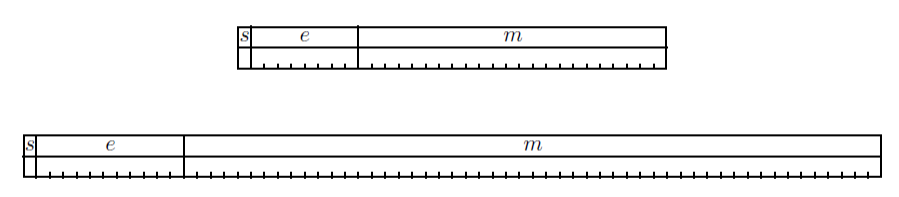
kitxmlcodelatexdvp\Large x=sm2^{e-d}finkitxmlcodelatexdvp- s est le signe, représenté par un seul bit, les 31, 63 ou 79 autres étant utilisés pour la valeur absolue du nombre (le complément n'est pas utilisé ici).
- m est la mantisse, c'est-à-dire un nombre inférieur à 1.0. On dit que le nombre est normalisé lorsque sa mantisse est comprise dans l'intervalle kitxmlcodeinlinelatexdvp[ 0.5 ; 1.0 [finkitxmlcodeinlinelatexdvp .
- e − d est l'exposant dont seule la partie e est stockée, alors que le décalage d est une constante caractéristique du type de variables. Cet artifice permet d'avoir des exposants négatifs tout en ne stockant que des valeurs positives de e.
La représentation des nombres réels dans des mots de 4 et 8 octets (32 et 64 bits) fait l'objet de la norme ANSI/IEEE Std 754-1985 (IEEE Standard for Binary Floating-Point Numbers), reprise par la suite par la CEI et l'ISO (tableau 2.6 et figure 2.1).
|
Type |
bit pour s |
bits pour e |
d |
bits pour m |
|---|---|---|---|---|
|
Real*4 |
1 |
8 |
126 |
23 (+1) |
|
Real*8 |
1 |
11 |
1022 |
52 (+1) |
Table 2.6 - Nombres de bits selon ANSI/IEEE Std 754-1985
La mention (+1) pour le nombre de bits réservés à la mantisse m appelle quelques explications : si le nombre est normalisé, sa mantisse est dans l'intervalle [ 0.5 ; 1.0 [ , son chiffre le plus significatif est obligatoirement un 1. On peut omettre de le mémoriser, c'est ce qu'on appelle le bit caché. Grâce à cette astuce, un champ de 23 ou 52 bits permet de stocker une mantisse dont on connaît 24 ou 53 bits.

2-4. Stockage des nombres complexes▲
Certains langages permettent de définir des variables comme complexes, et surtout, de généraliser l'utilisation des opérateurs arithmétiques aux nombres complexes.
Chaque nombre complexe est stocké comme deux nombres réels, la partie réelle et la partie imaginaire.
- Une variable de type Complex*8 occupe 8 octets : les 4 premiers pour la partie réelle et les 4 suivants pour la partie imaginaire.
- Une variable de type Complex*16 occupe 16 octets : les 8 premiers pour la partie réelle et les 8 suivants pour la partie imaginaire.
2-5. Stockage des tableaux▲
Le stockage des tableaux à plus d'un indice peut aussi donner lieu à des difficultés, car les différents langages ne procèdent pas de la même manière. En Fortran, c'est le premier indice qui varie le plus rapidement. Une matrice est donc stockée par colonnes. En C, c'est l'inverse : le dernier indice varie le plus rapidement. Une matrice est donc stockée par lignes.
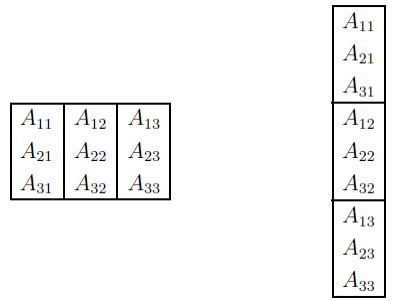
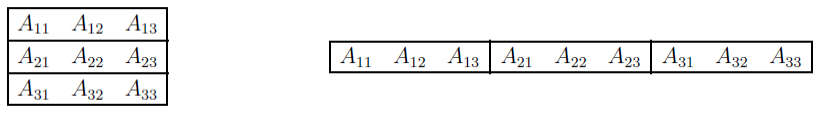
Il faut être conscient de cette différence lorsqu'on appelle un sous-programme en Fortran depuis un programme principal en C.
3. L'arithmétique de l'ordinateur▲
3-1. Arithmétique des nombres entiers▲
Avec les nombres entiers, les opérations d'addition, de soustraction et de multiplication donnent des résultats exacts pour autant qu'on ne sorte pas de l'étendue du type de variable considéré. Les dépassements éventuels peuvent conduire à des résultats imprévisibles, qui dépendent d'ailleurs du type de processeur et du langage de programmation. On sait en revanche que le quotient de deux nombres entiers n'est en général pas un nombre entier, élément de kitxmlcodeinlinelatexdvp\mathbb{Z}finkitxmlcodeinlinelatexdvp , mais un nombre rationnel, élément de kitxmlcodeinlinelatexdvp\mathbb{Q}finkitxmlcodeinlinelatexdvp . On est donc conduit à définir une nouvelle opération, la division entière :
kitxmlcodelatexdvp7 \ DIV \ 3\Rightarrow 2finkitxmlcodelatexdvpAinsi définie, la division entière donne aussi des résultats exacts. Il convient d'être attentif au fait que la multiplication n'est pas l'opération inverse de la division entière :
kitxmlcodelatexdvp3(7 \ DIV \ 3)\Rightarrow 6finkitxmlcodelatexdvp3-2. Arithmétique des nombres réels▲
Pour additionner deux nombres réels x et y (figure 3.1), le processeur commence, si les deux opérandes n'ont pas le même exposant, par dénormaliser le plus petit, c'est-à-dire décaler sa mantisse vers la droite d'un nombre de positions égal à la différence des exposants initiaux et à corriger son exposant en conséquence (figure 3.2).
Il additionne ensuite les mantisses (figure 3.3), ce qui peut faire apparaître sur la gauche un bit excédentaire de retenue.


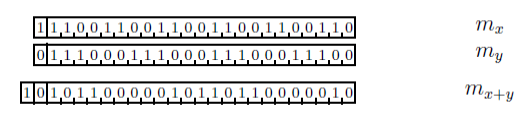
Pour éliminer ce bit excédentaire à gauche de la mantisse (le plus significatif), le résultat est renormalisé. Il en résulte un bit excédentaire à droite (le moins significatif). Comme, dans cet exemple, ce bit vaut 0, on peut le laisser tomber ou, en d'autres termes, arrondir le résultat sans que cela n'introduise d'erreur (figure 3.4).

En revanche, si le bit excédentaire à droite valait 1, le fait de le laisser tomber introduirait une erreur. La norme ANSI/IEEE Std 754-1985 règle le problème de l'arrondi selon trois possibilités .
- Si le bit excédentaire vaut 0, on le laisse simplement tomber.
- Si le bit excédentaire vaut 1 et si le bit précédent vaut 0, on arrondit vers le bas : on laisse tomber le bit excédentaire.
- Si le bit excédentaire et le(s) précédent(s) valent 1, on arrondit vers le haut, avec les retenues qui s'imposent.
3-3. Ce qui se passe réellement▲
La méthode d'arrondi préconisée par la norme ANSI/IEEE Std 754-1985 a l'avantage d'éviter le biais qui se produirait si on se contentait de tronquer les résultats, c'est-à-dire de les arrondir systématiquement vers le bas. En revanche, elle ralentit les calculs de manière significative. C'est pourquoi les constructeurs ont fait différents choix en ce qui concerne le respect ou non de la norme.
- La plupart des stations de travail Unix suivent strictement la norme.
- Certains superordinateurs privilégient la vitesse de calcul aux dépens de la précision et ne suivent pas la norme, se contentant de tronquer les résultats.
- Les processeurs Intel et compatibles constituent un cas à part : en interne, les calculs se font sur des registres de 80 bits, les résultats étant tronqués, mais pour les échanges avec la mémoire, les données sont raccourcies à 64 bits et arrondies selon la norme.
3-4. Étendue et précision▲
Le processeur considère qu'un nombre est infini lorsque tous les bits de son exposant sont mis à 1, et cela quel que soit le contenu de la mantisse. Le plus grand nombre fini que l'on peut stocker est donc celui dont tous les bits sont égaux à 1 sauf le dernier de l'exposant décalé e (et éventuellement celui de signe).

La représentation interne vue plus haut ne fonctionne que lorsque l'exposant e−d est supérieur au décalage d, c'est-à-dire lorsque e est strictement positif. La précision correspond aux nombres de bits de la mantisse (y compris le bit caché). Le plus petit nombre non nul que l'on peut stocker sans perte de précision est donc celui dont tous les bits sont égaux à 0, sauf le premier de la partie visible de la mantisse.

Il est possible de stocker des nombres encore plus petits, mais dans ce cas, le mode de représentation interne change : l'exposant e − d reste égal au décalage d, car e est nul et ne peut pas devenir négatif. Le bit caché n'est plus utilisé. La partie significative de la mantisse se raccourcit au fur et à mesure que le nombre devient plus petit. Il y a donc perte de précision. Le plus petit nombre non nul que l'on peut stocker avec perte de précision est donc celui dont seul le dernier bit vaut 1.
Remarque : selon le langage de programmation, le compilateur et les options de compilation, il peut arriver que toutes les valeurs trop petites pour être stockées sans perte de précision soient considérées comme véritablement nulles.

La notion de précision est fondamentalement différente de ce qui précède. Elle désigne par convention la différence entre le nombre 1.0 et chacun des nombres les plus proches de 1.0 qui puissent encore en être distingués.


4. Remerciements▲
Les commentaires et les suggestions d'amélioration sont les bienvenus alors après votre lecture, n'hésitez pas, Commentez1.
Nos remerciements à -Nikopol- et à LittleWhite pour leur relecture technique et à ced et à jacques_jean pour leur relecture orthographique.



