Résolution des systèmes linéaires

De nombreux problèmes numériques se ramènent d'une manière plus ou moins approchée à la résolution de systèmes d'équations linéaires. Un système linéaire d'ordre 4 :

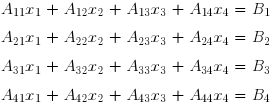
peut aussi être écrit sous forme matricielle :

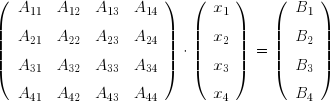
ou en notation abrégée :

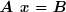
La matrice A et le vecteur B sont connus. La résolution du système consiste à calculer le vecteur des inconnues x . La matrice A et les vecteurs B et x peuvent être réels ou complexes.

La méthode de Cramer a été fréquemment enseignée dans les cours de mathématiques élémentaires. La valeur de chaque inconnue est exprimée explicitement comme le quotient de deux déterminants. On calcule tout d'abord le déterminant de la matrice A :

On remplace ensuite successivement chaque colonne de la matrice A par le vecteur B et on calcule les déterminants correspondants. On en déduit les valeurs des inconnues :

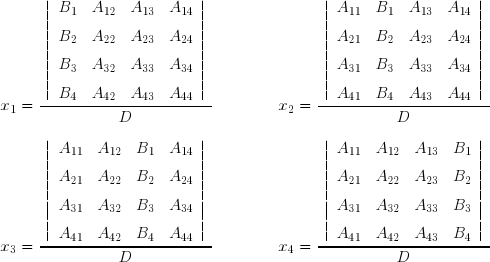
Une telle méthode utilisant des déterminants permet de faire une théorie générale des systèmes linéaires et de discuter l'existence et l'unicité de leurs solutions. En revanche, elle est totalement inadaptée pour la résolution numérique des gros systèmes linéaires, car le nombre d'opérations arithmétiques élémentaires et le temps de calcul augmentent comme la factorielle de l'ordre du système. Avec la méthode de Cramer, la résolution d'un système de 100 équations à 100 inconnues sur un super-ordinateur nécessiterait un temps de calcul supérieur à l'âge de l'univers, alors que le même travail peut être effectué en moins d'une seconde en utilisant une « bonne méthode ».

Les méthodes utilisables pour la résolution numérique de gros systèmes linéaires sont subdivisées en deux catégories :

• les méthodes directes où la solution est obtenue par un nombre d'opérations élémentaires fini et connu d'avance (le plus souvent un polynôme du 3^ème degré en l'ordre n du système): méthodes de substitution, méthode d'élimination de Gauss, factorisation LR par la méthode de Crout, factorisation QR, par la méthode de Householder, méthode de Cholesky, décomposition selon les valeurs singulières, etc. ;
• les méthodes itératives à l'aide desquelles on tend par approximations successives vers la solution: méthodes de Jacobi, de Gauss-Seidel, de sur-relaxation, des gradients conjugués, etc.

La bonne stratégie consiste à choisir les algorithmes en fonction des particularités éventuelles de la matrice du système à résoudre. Les critères de choix seront, entre autres :

• la place occupée en mémoire ;
• le temps de calcul ;
• l'exactitude des résultats.

Les méthodes générales donnent, dans l'ensemble, des résultats satisfaisants, mais l'effort de mise en œuvre d'algorithmes plus subtils est presque toujours récompensé.