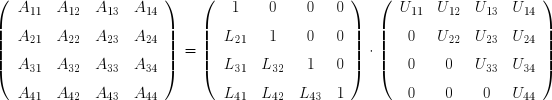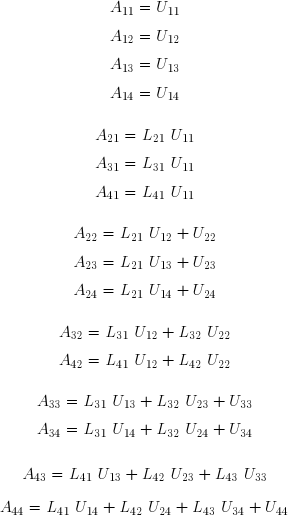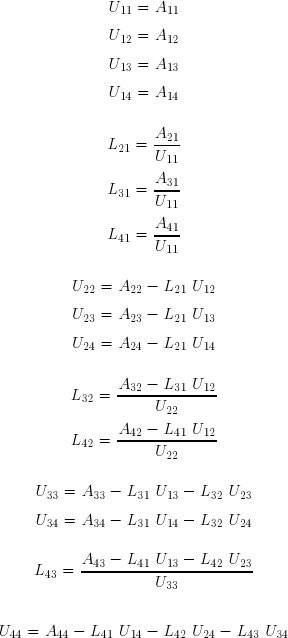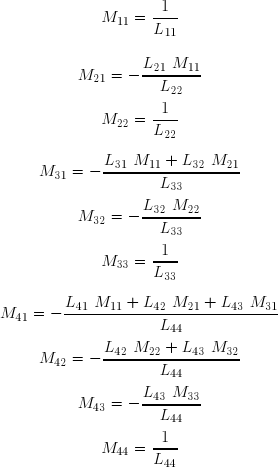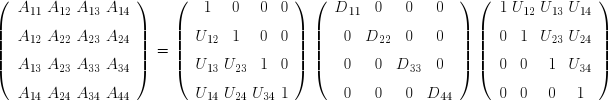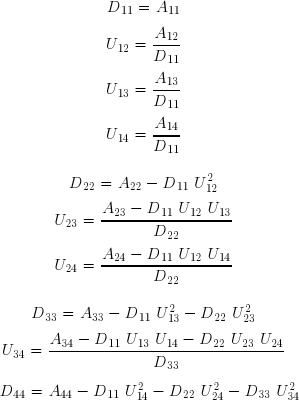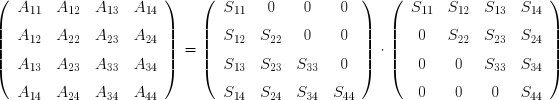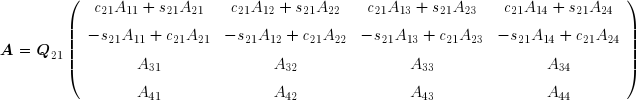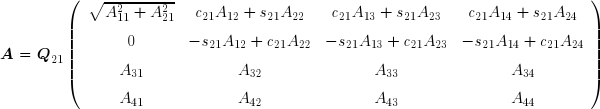II. Méthodes directes▲
II-A. Systèmes avec matrice triangulaire▲
Il peut arriver que la matrice du système soit triangulaire, c'est-à-dire que tous les termes situés d'un côté de la diagonale principale soient nuls. Selon le côté, on parlera de matrice triangulaire inférieure ( L , en anglais: lower ou left ) :
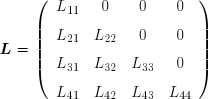
ou de matrice triangulaire supérieure ( U , en anglais: upper , ou R , en anglais: right ) :
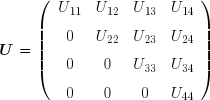
Lorsque la matrice d'un système linéaire est triangulaire, les calculs pour sa résolution sont grandement simplifiés. Prenons tout d'abord le cas d'une matrice triangulaire inférieure gauche. Le système s'écrit :
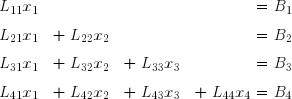
Le calcul de x1 est immédiat :
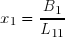
La valeur de x1 étant maintenant connue, on peut l'introduire dans les trois équations restantes et passer à droite les termes connus. :
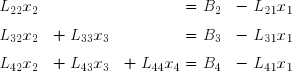
C'est maintenant le calcul de x2 qui est immédiat :
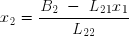
La valeur de x2 étant calculée, on peut l'introduire dans les deux équations restantes et passer à droite les termes connus :
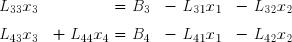
On a donc, de manière analogue :
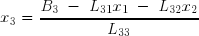
puis :
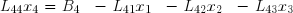
et enfin :
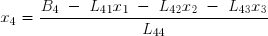
Il va sans dire que cet algorithme ne peut fonctionner que si la matrice n'est pas singulière, c'est-à-dire si aucun des termes diagonaux n'est nul. Dans le cas exposé ci-dessus, les coefficients situés sur la diagonale principale sont quelconques. Dans d'autres cas, et en particulier lors de l'utilisation de la méthode de Crout, que nous verrons ultérieurement, on sait à l'avance que tous ces coefficients sont obligatoirement égaux à l'unité. Il est par conséquent inutile de les stocker, de tester s'ils sont nuls et de diviser par leur valeur.
Dans le cas où la matrice est triangulaire supérieure droite, et non plus inférieure gauche, on procède de la même manière, mais en commençant par la dernière équation et la dernière inconnue.
Le fait que la matrice d'un système linéaire soit triangulaire est une circonstance très favorable pour sa résolution : le nombre d'opérations élémentaires et le temps de calcul augmentent comme un polynôme du 2ème degré en l'ordre n du système). Les méthodes de substitution sont donc très rapides.
Malheureusement, les problèmes qui conduisent à des systèmes aussi simples à résoudre sont plutôt rares. Un certain nombre de méthodes « directes » ont pour but de transformer un système dont la matrice est quelconque en un système qui admet les mêmes solutions et dont la matrice est triangulaire.
II-B. Systèmes avec matrice orthogonale▲
II-B-1. Vecteurs orthogonaux en algèbre linéaire▲
En algèbre linéaire, on fait la distinction entre les vecteurs-lignes qui sont des matrices à une seule ligne :
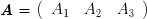
et les vecteurs-colonnes qui sont des matrices à une seule colonne :
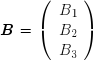
La transposée d'un vecteur-ligne est un vecteur-colonne :
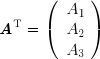
tandis que la transposée d'un vecteur-colonne est un vecteur-ligne :
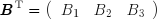
En vertu des règles qui régissent le produit matriciel, il n'est pas possible de multiplier deux vecteurs-lignes ou deux vecteurs-colonnes. En revanche, on peut définir le produit scalaire ou produit intérieur :

et le produit extérieur :
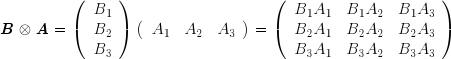
On appelle carré scalaire du vecteur-ligne A la grandeur :
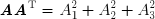
et du vecteur-colonne B la grandeur :
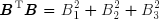
En vertu du théorème de Pythagore, la norme euclidienne d'un vecteur-ligne ou d'un vecteur-colonne est égale à la racine carrée de son carré scalaire :
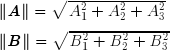
On dit que deux vecteurs-lignes A et C de normes non nulles sont orthogonaux lorsque leur produit scalaire est nul :
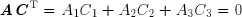
De manière analogue, on dit que deux vecteurs-colonnes B et D de normes non nulles sont orthogonaux lorsque leur produit scalaire est nul :
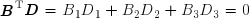
II-B-2. Matrices orthogonales▲
Une matrice réelle Q est dite orthogonale si et seulement si tous ses vecteurs-lignes sont orthogonaux entre eux et de norme unité. Il en est de même pour les vecteurs-colonnes. De cette définition il résulte que le produit d'une matrice orthogonale et de sa transposée donne la matrice unité 1 :
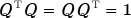
et, par conséquent, que l'inverse d'une matrice orthogonale est identique à sa transposée :
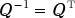
Le fait que la matrice d'un système linéaire soit orthogonale est une circonstance très favorable pour sa résolution puisque celle-ci se résume au produit de la transposée de la matrice et du vecteur de second membre.

Le nombre d'opérations élémentaires et le temps de calcul augmentent comme un polynôme du 2 ème degré en l'ordre n du système.
II-C. Méthode d'élimination de Gauss▲
La méthode d'élimination de Gauss utilise la propriété suivante :
- A toute équation d'un système linéaire on peut ajouter une combinaison linéaire quelconque des autres équations sans que cela ne change les valeurs des solutions.
En utilisant de manière judicieuse cette propriété, il est possible d'annuler successivement tous les termes situés sous la diagonale de la matrice, et ainsi de la transformer par étapes en une matrice triangulaire supérieure droite.
Soit le système
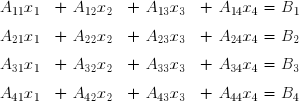
On soustrait de chaque terme de la deuxième équation le terme correspondant de la première, préalablement multiplié par A21/A11 . Le terme qui figure au dénominateur, ici A11 , est appelé pivot . Il va sans dire que la division ne peut être effectuée que si le pivot n'est pas nul. Les divers termes de la deuxième équation deviennent :
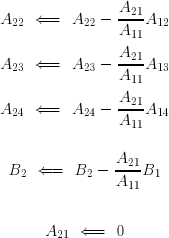
On procède de la même manière avec la troisième équation :
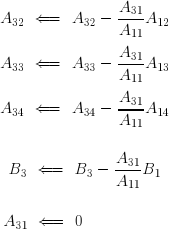
On procède encore de même avec la quatrième équation :
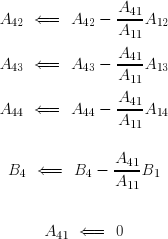
Après ces opérations, le système a pris la forme :
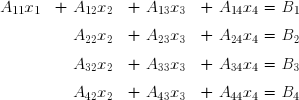
Il s'agit maintenant d'éliminer les coefficients A32 et A42 . Pour ce faire, on soustrait de chaque terme de la troisième équation le terme correspondant multiplié par A32/A22 . Les divers termes de la troisième équation deviennent :
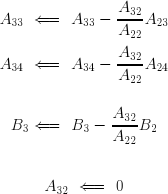
On procède de la même manière avec la quatrième équation :
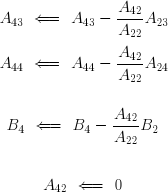
Après ces opérations, le système a pris la forme :

Il reste encore à éliminer le coefficient A43. Pour ce faire, on soustrait de chaque terme de la quatrième équation le terme correspondant multiplié par A43/A33. Les divers termes de la quatrième équation deviennent :
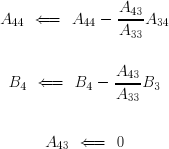
Le système a maintenant pris la forme voulue : sa matrice est triangulaire supérieure droite.
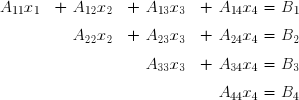
Il peut donc être résolu par la méthode de substitution vue plus haut. Le nombre d'opérations élémentaires et le temps de calcul augmentent comme un polynôme du 3ème degré en l'ordre n du système.
II-D. Systèmes mal conditionnés▲
Lorsqu'on étudie la résolution des systèmes linéaires d'un point de vue purement théorique, on distingue le cas où la matrice est régulière, qui conduit à une solution unique, et le cas où la matrice est singulière, d'où aucune solution ou une infinité de solutions. Lorsqu'il s'agit de résolution numérique, un cas supplémentaire doit être envisagé: la matrice peut être « presque singulière ».
Chacune des équations d'un système linéaire d'ordre n définit un hyperplan à n-1 dimensions dans un espace à n dimensions. La solution est représentée par les coordonnées de l'intersection de ces n hyperplans. Dans le cas d'un système d'ordre 2, il s'agit de l'intersection de 2 droites dans le plan.
Considérons tout d'abord une matrice régulière et bien conditionnée, comme par exemple celle du système :
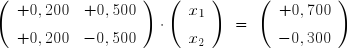
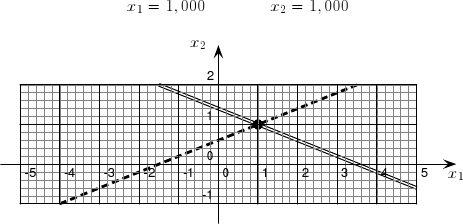
Les deux droites se coupent de manière franche et on a une solution bien déterminée :
Si la matrice est singulière, cela implique que les deux droites ont la même pente. Pour le système :
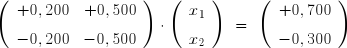
elles sont parallèles. Le système n'admet donc aucune solution.
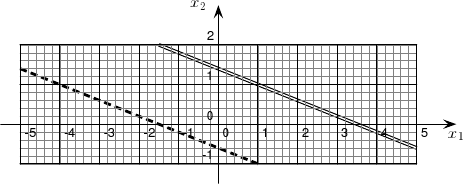
En revanche, pour le système ayant la même matrice mais des seconds membres différents :
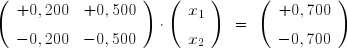
elles sont confondues. Le système admet donc une infinité de solutions.
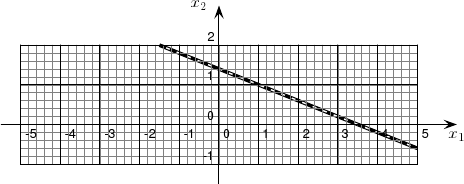
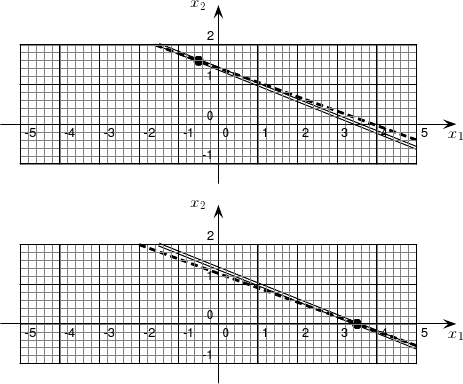
Considérons maintenant deux systèmes ayant la même matrice et des seconds membres très peu différents :
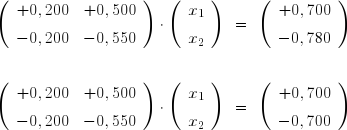
Leurs matrices sont presque singulières. Les équations définissent donc des droites qui se coupent sous un angle très aigu.
On voit que de très petites différences dans les seconds-membres conduisent à des solutions très différentes, puisqu'on a pour l'un des systèmes x1 = -0,500 et x2 = 1,600 et pour l'autre x1 = 3,500 et x2 = 0,000
On voit qu'un tel système est très sensible à de petites variations du second-membre. On dit que sa matrice est mal conditionnée . Le plus souvent, la cause de ce mauvais conditionnement réside dans une maladresse lors de la mise en équations du problème physique. S'il n'est pas possible de l'éviter, parce que le problème est intrinsèquement instable, il faudra utiliser une méthode de résolution plus stable, mais plus coûteuse que la méthode de Gauss.
On définira plus loin un estimateur du conditionnement Rcond qui permet d'exprimer de manière chiffrée si une matrice est plus ou moins mal conditionnée. Cet estimateur vaut 1 si tous les hyperplans correspondant aux équations sont perpendiculaires. Il est nul si la matrice est singulière. S'il est du même ordre de grandeur que la précision de calcul, on doit considérer la matrice comme tellement mal conditionnée que les résultats perdront, dans la plupart des cas, toute signification.
II-E. Échange de pivots▲
L'ordre dans lequel on range les équations et celui dans lequel on numérote les inconnues sont en principe indifférents. Deux raisons peuvent nous conduire à permuter des équations ou des inconnues :
- Nous avons vu que le mécanisme d'élimination faisait intervenir une division par chaque terme diagonal, appelée aussi pivot . Cette opération n'est évidemment possible que si le pivot n'est pas nul. Si l'on tombe sur un pivot nul, il est possible de contourner la difficulté en permutant l'équation où il se trouve avec une des suivantes. Si, à la fin de l'élimination de Gauss, il reste un pivot nul lorsque plus aucune permutation n'est possible, cela signifie que la matrice est singulière ;
- On constate d'autre part que, pour la détermination de chaque nouveau coefficient, on calcule la différence de l'ancienne valeur de ce coefficient et d'un terme qui est le produit de deux coefficients divisé par le pivot. Ce terme est entaché d'une erreur d'arrondi résultant de la multiplication et de la division. Pour que l'erreur relative sur la différence soit minimale, il faut que ce terme soit le plus petit possible en comparaison de l'ancienne valeur. Cela signifie que l'ordre optimal des équations et des inconnues est celui qui conduit à diviser par des pivots de plus grande valeur absolue.
Il est en principe possible d'échanger aussi bien les équations que les inconnues. On parle de pivotage partiel lorsqu'on n'échange que les équations et de pivotage complet lorsqu'on échange aussi bien les inconnues que les équations. On peut démontrer que si la matrice du système est régulière, la méthode de Gauss avec pivotage partiel est toujours exécutable et fournit des résultats presque aussi bons qu'avec le pivotage complet. C'est pourquoi le pivotage complet, beaucoup plus lourd, n'est presque jamais utilisé. En revanche, le pivotage partiel est essentiel si la matrice du système est mal conditionnée ou si son ordre est élevé.
II-F. Factorisation LU (méthode de Crout)▲
Il arrive fréquemment que l'on ait à résoudre plusieurs systèmes linéaires présentant la même matrice des coefficients A, mais des seconds-membres B différents. Si tous ces vecteurs B sont connus a priori, la méthode d'élimination de Gauss permet de résoudre simultanément les divers systèmes. Dans d'autres cas, chaque second-membre est calculé à partir de la solution du système précédent. La factorisation LU permet de n'effectuer qu'une fois la partie la plus coûteuse des calculs. La méthode repose sur le fait que toute matrice régulière peut être mise sous la forme du produit d'une matrice triangulaire inférieure gauche L dont tous les termes diagonaux sont égaux à l'unité et d'une matrice triangulaire supérieure droite U.
Effectuons littéralement le produit matriciel, soit :
Ces relations permettent de déterminer successivement les termes des deux matrices triangulaires :
On remarquera que la méthode de Crout ne nécessite pas l'utilisation de tableaux auxiliaires autres que celui utilisé à l'entrée pour le stockage de la matrice originale A et à la sortie pour le stockage des deux matrices triangulaires L et U.
Sous forme matricielle condensée, le système :
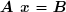
devient :
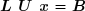
On définit maintenant le vecteur auxiliaire :
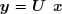
Le système peut alors être résolu par deux applications successives de la méthode de substitution, tout d'abord en avant à :

puis en arrière à :

Il convient encore de remarquer que, sans qu'il n'y paraisse de manière évidente, les méthodes de Crout et de Gauss sont équivalentes: la matrice U est identique à la matrice triangulaire obtenue par la méthode d'élimination de Gauss. C'est pourquoi certaines bibliothèques de sous-programmes intitulent "élimination de Gauss" des sous-programmes qui effectuent en fait une factorisation LU.
II-G. Factorisation LU avec échange de pivots▲
Pour la factorisation LU, l'échange de pivots se fait de la même manière que pour la méthode d'élimination de Gauss. Les permutations de lignes qui sont effectuées doivent naturellement être mémorisées. Cela peut se faire dans une matrice de permutation P ; une telle matrice contient des termes égaux à 1, à raison d'un seul par ligne et un seul par colonne, tous les autres termes étant nuls. On a alors :
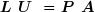
II-H. Raffinement itératif de la solution▲
Il est évident qu'un système linéaire ne peut pas être résolu avec une précision meilleure que celle de l'ordinateur utilisé. Malheureusement, pour de gros systèmes, il est souvent difficile d'atteindre, voire d'approcher cette précision. Avec les méthodes directes, comme la méthode d'élimination de Gauss, les erreurs d'arrondis s'accumulent, et cela d'autant plus que la matrice est plus mal conditionnée. Le raffinement itératif de la solution est une technique qui permet de retrouver la précision de l'ordinateur utilisé. Soit le système linéaire :
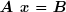
La méthode d'élimination de Gauss ne nous donne pas la solution exacte x mais une solution approchée :
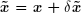
où ![]() est l'erreur inconnue. En multipliant la matrice A par la solution approchée, on obtient un vecteur :
est l'erreur inconnue. En multipliant la matrice A par la solution approchée, on obtient un vecteur :
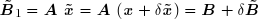
d'où par soustraction :
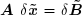
La méthode d'élimination de Gauss, appliquée à ce nouveau système ne nous donne pas la valeur exacte ![]() de l'erreur commise précédemment, mais une valeur approchée
de l'erreur commise précédemment, mais une valeur approchée ![]() . Par soustraction, on obtient :
. Par soustraction, on obtient :
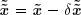
qui est une meilleure approximation de x . Le procédé peut être répété plusieurs fois. L'utilisation de la méthode de Crout, plutôt que de la méthode d'élimination de Gauss, est particulièrement avantageuse lorsqu'on prévoit de devoir procéder au raffinement itératif de la solution. En effet, il suffit de n'exécuter qu'une fois la factorisation, qui est la partie la plus longue de la résolution.
II-I. Inversion d'une matrice▲
Contrairement à ce qu'on lit parfois, il est rarement utile de calculer numériquement l'inverse d'une matrice. Mais lorsque c'est nécessaire, il est aisé de l'obtenir à l'aide des matrices L et U. Montrons tout d'abord comment on peut calculer M = L-1, on sait que :
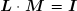
où I est la matrice identité de mêmes dimensions que L . On montre facilement que M est aussi triangulaire inférieure gauche.
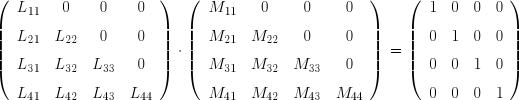
Effectuons littéralement le produit matriciel, soit :
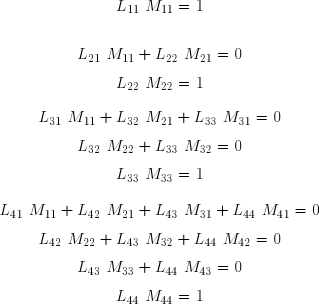
On en tire les termes de M :
On procède de manière analogue pour V = U-1. On a pour terminer :

II-J. Calcul d'un déterminant▲
Avant d'entreprendre le calcul d'un déterminant, il convient de se demander à quoi cela va servir. Si c'est seulement pour s'assurer qu'une matrice est régulière, il est beaucoup plus simple et rapide d'essayer la méthode de Crout: si, malgré toutes les permutations, il subsiste un pivot nul, cela signifie que la matrice est singulière.
On peut sérieusement douter de la signification physique du déterminant d'une matrice: en effet, si, par exemple les termes d'une matrice d'ordre n sont exprimés en ohms, son déterminant sera exprimé en ohms à la puissance n . Si malgré cela la valeur du déterminant doit véritablement être trouvée, il faut éviter à tout prix la méthode consistant à sommer des produits de termes et de leurs mineurs: le temps de calcul est proportionnel à la factorielle de la taille de la matrice. On peut procéder beaucoup plus simplement si la matrice a été factorisée, sachant que :
- le déterminant du produit de deux matrices est égal au produit de leurs déterminants ;
- le déterminant d'une matrice triangulaire est égal au produit de ses termes diagonaux.
On aura donc :

d'où :
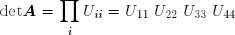
Il faut prendre garde au fait que, si la matrice est grande, son déterminant peut devenir très grand ou très petit, et provoquer un dépassement de capacité vers le haut ou vers le bas.
II-K. Matrices symétriques et matrices hermitiennes▲
Dans le cas des matrices réelles symétriques et des matrices complexes symétriques ou hermitiennes, les calculs peuvent être effectués d'une manière plus efficace.
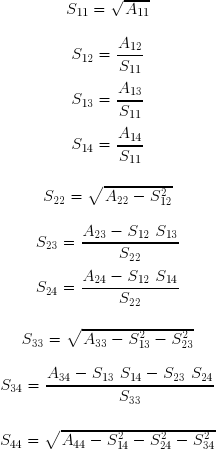
Prenons le cas d'une matrice réelle symétrique A. Elle peut être transformée en le produit d'une matrice triangulaire supérieure droite U dont tous les termes diagonaux sont égaux à l'unité, de sa transposée UT et d'une matrice diagonale D.
Effectuons littéralement le produit matriciel, soit :
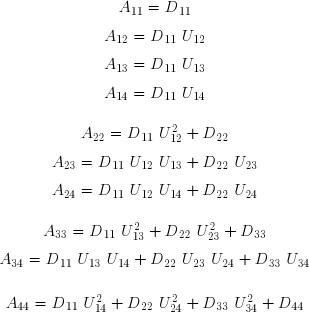
Ces relations permettent de déterminer successivement les termes de la matrice diagonale et de la matrice triangulaire :
Sous forme matricielle condensée, le système :
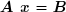
devient :
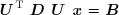
On définit les vecteurs auxiliaires :
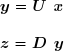
Le système peut alors être résolu par deux applications successives de la méthode de substitution et une division par une matrice diagonale :
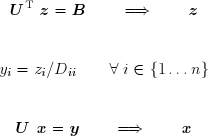
Notons que le pivotage doit être complet (permutation simultanée des lignes et des colonnes) si l'on désire conserver la symétrie de la matrice.
Le cas des matrices complexes symétriques et des matrices hermitiennes se traitent de manière analogue.
II-L. Méthode de Cholesky▲
On rencontre souvent des problèmes qui conduisent à résoudre un système linéaire dont la matrice est symétrique et définie positive (toutes ses valeurs propres sont strictement positives). On démontre qu'une telle matrice peut être mise sous la forme du produit d'une matrice triangulaire supérieure droite S et de sa transposée ST.
Effectuons littéralement le produit matriciel, soit :
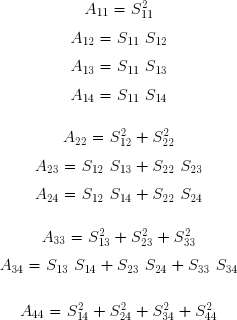
Ces relations permettent de déterminer successivement les termes de la matrice triangulaire :
Sous forme matricielle condensée, le système :
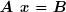
devient :
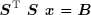
On définit le vecteur auxiliaire :
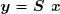
Le système peut alors être résolu par deux applications successives de la méthode de substitution, tout d'abord à :

puis à :

La méthode de Cholesky est presque deux fois plus rapide que la méthode d'élimination de Gauss. La question est de savoir, de cas en cas, si on est en droit de l'utiliser. Pour s'en assurer, il suffit de vérifier, au fur et à mesure de la factorisation, que l'argument des racines carrées est toujours strictement positif. D'autre part, de nombreux problèmes physiques reviennent à chercher le minimum d'une forme quadratique , c'est-à-dire d'une expression de la forme :
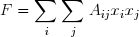
Pour annuler les dérivées partielles par rapport à chacune des variables indépendantes, on doit résoudre un système linéaire dont la matrice est nécessairement symétrique définie positive. Le nombre d'opérations élémentaires et le temps de calcul augmentent comme un polynôme du 3ème degré en l'ordre n du système.
II-M. Factorisation QR (méthode de Householder)▲
Comme vu précédemment, une matrice Q est orthogonale si :
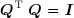
Il résulte de cette définition que l'inverse d'une matrice orthogonale est identique à sa transposée :

La solution d'un système linéaire de la forme :
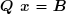
s'obtient en multipliant le vecteur des seconds-membres B par la transposée de la matrice Q :
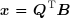
Le nombre d'opérations élémentaires et le temps de calcul augmentent comme un polynôme du 2ème degré en l'ordre n du système.
La méthode de Householder consiste à écrire la matrice A comme le produit d'une matrice orthogonale Q et d'une matrice triangulaire supérieure droite que nous appellerons R pour ne pas la confondre avec celle obtenue par la méthode de Crout.
La factorisation QR obéit à la relation :
La méthode de fractionnement repose sur deux faits :
- la matrice décrivant une rotation est orthogonale ;
- le produit de matrices orthogonales est encore une matrice orthogonale.
On pose tout d'abord :
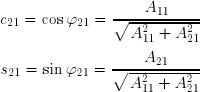
où ![]() représente un angle de rotation. On peut écrire :
représente un angle de rotation. On peut écrire :
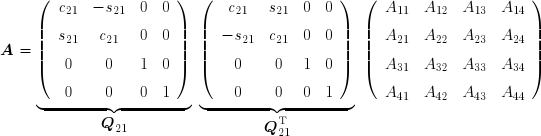
Effectuons le produit de droite :
que l'on peut transformer en appliquant :
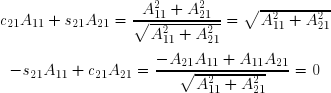
Il s'ensuit que :
Comme on le voit, on a annulé le terme 21. De manière analogue, il est possible d'annuler successivement tous les termes situés au-dessous de la diagonale principale à l'aide de matrices de rotation Q31, Q41, Q32, Q42 et Q43 . On a ainsi transformé la matrice A en une matrice triangulaire supérieure droite R . La matrice orthogonale Q est le produit des matrices de rotation élémentaires :
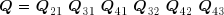
Sous forme matricielle condensée, le système :
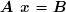
devient :
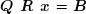
On définit le vecteur auxiliaire :
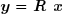
Le système peut alors être résolu en résolvant tout d'abord :
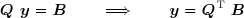
puis :

Le nombre d'opérations élémentaires et le temps de calcul sont à peu près le double de ceux qu'on aurait avec la méthode d'élimination de Gauss. C'est pourquoi la factorisation QR n'est utilisée que dans des cas spéciaux.
II-N. Factorisation SVD (valeurs singulières)▲
Pour une matrice A quelconque, on appelle valeur singulière et vecteurs singuliers correspondants un scalaire non négatif s et deux vecteurs ![]() et
et ![]() tels que :
tels que :
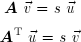
On regroupe les vecteurs singuliers ![]() et
et ![]() en deux matrices U et V et les valeurs singulières, par ordre décroissant s en une matrice diagonale S :
en deux matrices U et V et les valeurs singulières, par ordre décroissant s en une matrice diagonale S :
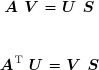
Il s'ensuit que :
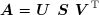
Pour résoudre le système :
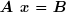
on calcule les matrices U , S et V . Le système devient :
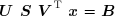
On définit les vecteurs auxiliaires :
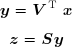
Le système peut être résolu en résolvant successivement :
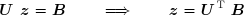
puis :
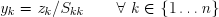
et enfin :
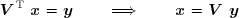
On appelle pseudo-inverse de Moore-Penrose le produit M = VS-1UT.
La solution du système est donc :
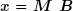
La méthode des valeurs singulières est plus coûteuse en temps et en place en mémoire que celles que nous avons vues précédemment, mais c'est aussi la plus stable, c'est-à-dire la plus précise, même sans utiliser le raffinement itératif ; c'est pourquoi on ne l'utilise que dans les cas exceptionnels où aucune des autres méthodes n'est applicable.