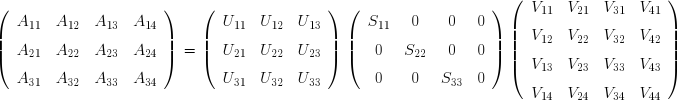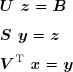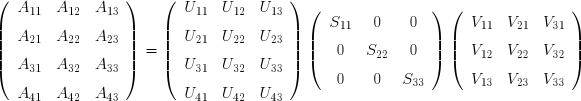III. Problèmes pathologiques▲
Cette section montre comment faire face à des situations dues à trois formulations d'une même loi fondamentale :
Loi de Murphy S'il y a plus d'une façon de faire quelque chose, et que l'une d'elles conduit à un désastre, alors il y aura quelqu'un pour le faire de cette façon ;
Loi de Finagle Si quelque chose de mal peut se produire, cela arrivera ;
Loi de la tartine beurrée Une tartine beurrée tombe toujours sur le côté beurré.
Dans cette perspective, nous étudierons divers cas :
- la matrice est carrée et singulière : système indéterminé ;
- la matrice est carrée et singulière : système impossible ;
- la matrice est carrée et mal conditionnée ;
- la matrice est rectangulaire : plus d'inconnues que d'équations ;
- la matrice est rectangulaire : plus d'équations que d'inconnues.
III-A. Matrice singulière ; système indéterminé▲
On considère le système linéaire A x = B dont la matrice A est singulière.
La factorisation LU ne fonctionne pas car on tombe inévitablement sur un pivot nul. La factorisation QR peut être réalisée, mais conduit à une matrice R dont au moins un terme diagonal est nul ; c'est alors la substitution arrière qui tombe sur une division par zéro.
Méthode SVD▲
La factorisation peut toujours être réalisée. Si la matrice A est singulière, alors une ou plusieurs des valeurs singulières, stockées sur la diagonale principale de la matrice S sont nulles.
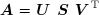
On définit les vecteurs auxiliaires y et z en posant :
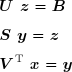
La matrice U étant orthogonale, le calcul du vecteur z ne pose aucun problème :
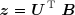
Pour déterminer chaque composante y k du vecteur y , on doit diviser la composante zk du vecteur z par la valeur singulière correspondante Sk , ce qui est évidemment impossible si celle-ci est nulle. On alors recours à l'astuce suivante : on met à zéro la composante yk qui sans cela serait infinie, résultant d'une division par zéro.
Pour k de 1 à n
Si S(k) plus grand que zéro
y(k) = z(k)/S(k)
Sinon
y(k) = 0
Fin Si
Fin PourLa matrice V étant orthogonale, le calcul du vecteur x ne pose aucun problème :
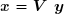
Il peut sembler choquant de remplacer l'inverse de zéro par zéro lui-même. En fait, parmi l'infinité de solutions qui satisfont le système à résoudre, x est celle dont la norme euclidienne est la plus petite.
III-B. Matrice singulière ; système impossible▲
On considère le système linéaire Ax = B dont la matrice A est singulière.
La factorisation LU ne fonctionne pas car on tombe inévitablement sur un pivot nul. La factorisation QR peut être réalisée, mais conduit à une matrice R dont au moins un terme diagonal est nul; c'est alors la substitution arrière qui tombe sur une division par zéro.
Méthode SVD▲
La factorisation peut toujours être réalisée. Si la matrice A est singulière, alors une ou plusieurs des valeurs singulières, stockées sur la diagonale principale de la matrice S sont nulles.
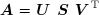
On définit les vecteurs auxiliaires y et y en posant :
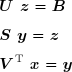
La matrice U étant orthogonale, le calcul du vecteur z ne pose aucun problème :
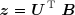
Pour déterminer chaque composante y k du vecteur y , on doit diviser la composante zk du vecteur z par la valeur singulière correspondante Sk , ce qui est évidemment impossible si celle-ci est nulle. On alors recours à l'astuce suivante: on met à zéro la composante yk qui sans cela serait infinie, résultant d'une division par zéro.
Pour k de 1 à n
Si S(k) plus grand que zéro
y(k) = z(k)/S(k)
Sinon
y(k) = 0
Fin Si
Fin PourLa matrice V étant orthogonale, le calcul du vecteur x ne pose aucun problème :
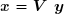
Il peut sembler choquant de remplacer l'inverse de zéro par zéro lui-même. En fait, aucune solution ne satisfait exactement le système à résoudre, mais le vecteur trouvé x est celui qui la satisfait le moins mal, c'est-à-dire celui pour lequel la norme euclidienne de Ax - B est la plus petite.
III-C. Matrice carrée mal conditionnée▲
On considère le système linéaire Ax = B dont la matrice A est mal conditionnée.
Méthode SVD▲
La factorisation peut toujours être réalisée :
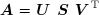
On définit les vecteurs auxiliaires y et z en posant :
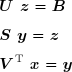
Si la matrice A est mal conditionnée, alors les dernières valeurs singulières, stockées au bas de la diagonale principale de la matrice S sont très petites par rapport à la plus grande. La matrice U étant orthogonale, le calcul du vecteur z ne pose aucun problème :
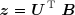
Pour déterminer chaque composante yk du vecteur y , on doit diviser la composante z k du vecteur z par la valeur singulière correspondante Sk , ce qui donnerait un résultat démesuré si celle-ci est très petite. On alors recours à l'astuce suivante : on met à zéro la composante yk qui sans cela serait démesurée, résultant d'une division par une valeur singulière très petite.
Pour k de 1 à n
Si S(k) plus grand que epsilon*S(1)
y(k) = z(k)/S(k)
Sinon
y(k) = 0
Fin Si
Fin PourLa matrice V étant orthogonale, le calcul du vecteur x ne pose aucun problème :
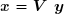
Il peut sembler choquant de remplacer l'inverse d'un nombre très petit par zéro. En fait, c'est cette manière de faire qui donne les résultats les plus raisonnables.
III-D. Matrices rectangulaires : systèmes sous-déterminés▲
On considère le système linéaire A x = B dont la matrice A comporte m lignes et n colonnes, avec m<n :
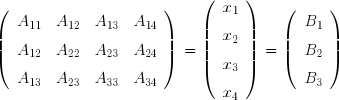
Certaines des méthodes vue jusqu'ici ne s'appliquent, du fait de leur principe même, qu'à des matrices carrées (substitution, élimination de Gauss, factorisation LU, méthode de Cholesky). D'autres, en revanche, peuvent aussi être utilisées pour des matrices rectangulaires.
Méthode QR▲
La factorisation QR donne une matrice orthogonale carrée Q à m lignes et m colonnes, et une matrice « trapézoïdale » R à m lignes et n colonnes :
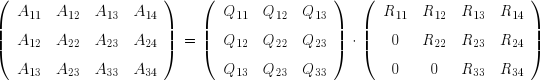
On définit le vecteur auxiliaire y en posant :
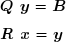
La matrice Q étant orthogonale, le calcul du vecteur y ne pose aucun problème :
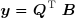
En revanche, la matrice R ayant moins de lignes que de colonnes, la solution du système Rx = y est indéterminée. On contourne la difficulté en attribuant une valeur arbitraire (souvent zéro) à une (ou éventuellement plusieurs) inconnue(s), en général la(les) dernière(s), puis on calcule les autres par la méthode de substitution.
Méthode SVD▲
La factorisation SVD donne :
On définit les vecteurs auxiliaires y et z en posant :
III-E. Matrices rectangulaires : systèmes surdéterminés▲
Dans les systèmes surdéterminés, on a plus d'équations que d'inconnues. La matrice A a donc un nombre de lignes m supérieur au nombre de colonnes n :
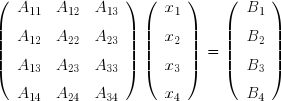
Méthode QR▲
La factorisation QR donne :
La matrice Q est carrée; elle a m lignes et m colonnes. La matrice R est rectangulaire; elle a m lignes et n colonnes; tous les termes de la dernière ligne sont nuls.
Méthode SVD▲
La factorisation SVD donne :
La matrice U est rectangulaire; elle a m lignes et n colonnes. La matrice S est diagonale; elle comporte n termes La matrice V est carrée; elle a n lignes et n colonnes.