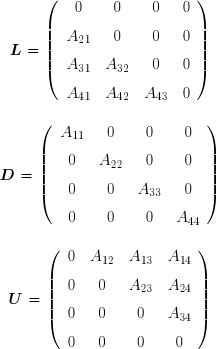IV. Méthodes itératives▲
IV-A. Méthode de Jacobi▲
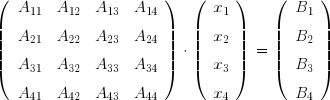
La méthode de Jacobi est une méthode itérative de résolution de système linéaire de la forme A x = B où :
Pour cela, on va construire une suite de vecteurs :
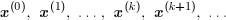
qui converge vers x , solution du système d'équations linéaires.
Remarque : chacun des vecteurs successifs est identifié par un numéro placé en exposant et entre parenthèses.
Algorithme▲
Un vecteur initial x(0) étant donné, l'algorithme suivant permet de déterminer les éléments successifs de la suite.
On décompose la matrice A en trois matrices L , D et U . La matrice L est constituée des termes qui se trouvent au-dessous de la diagonale principale de A(j < i) ; la matrice D contient les termes diagonaux de A(j = i) ; la matrice U est constituée des termes qui se trouvent au-dessus de la diagonale principale de A(j > i) .
Le système à résoudre peut alors s'écrire :
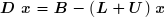
d'où l'on tire la formule de récurrence :
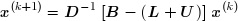
qui permet de calculer x(k+1) lorsque x(k) est connu :
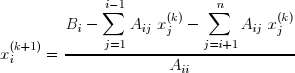
On remarquera que toutes les composantes de x(k) sont utilisées pour le calcul de chaque composante de x(k+1) . Ces deux vecteurs doivent donc être stockés dans deux tableaux distincts.
Erreur▲
A chaque itération, le vecteur trouvé x(k+1) comporte une certaine erreur :
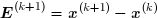
On pose P = D -1 (L+U) . Il vient alors :
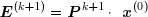
Convergence▲
L'algorithme converge si 
ou, ce qui revient au même, 
.
Théorème : une condition nécessaire et suffisante pour que est que les modules de toutes les valeurs propres de P soient strictement inférieures à 1.
Théorème : la formule de récurrence converge, quel que soit x(0) , si la matrice A est à diagonale dominante, c'est-à-dire si la valeur absolue de chaque terme diagonal est supérieure à la somme des valeurs absolues des termes rectangles placés sur la même ligne.
Résidu▲
On appelle résidu le vecteur R (k) = B - A x (k) . La précision exigée 
étant donnée, on arrête les itérations lorsque :
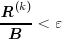
IV-B. Méthode de Gauss-Seidel▲
La méthode de Gauss-Seidel est une méthode itérative de résolution de système linéaire de la forme A x = B où :
Pour cela, on va construire une suite de vecteurs :
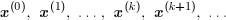
qui converge vers x , solution du système d'équations linéaires.
Remarque : chacun des vecteurs successifs est identifié par un numéro placé en exposant et entre parenthèses.
Algorithme▲
Un vecteur initial x(0) étant donné, l'algorithme suivant permet de déterminer les éléments successifs de la suite.
On décompose la matrice A en trois matrices L , D et U . La matrice L est constituée des termes qui se trouvent au-dessous de la diagonale principale de A(j < i) ; la matrice D contient les termes diagonaux de A(j = i) ; la matrice U est constituée des termes qui se trouvent au-dessus de la diagonale principale de A(j > i) .
Le système à résoudre peut alors s'écrire :
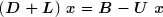
d'où l'on tire la formule de récurrence :
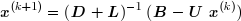
qui permet de calculer les composantes de x(k+1) lorsque celles de x sont connues :
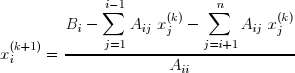
On remarquera que chaque composante de x(k) n'est utilisée que jusqu'au calcul de la composante correspondante de x(k+1) . Ces deux vecteurs peuvent donc être stockés dans le même tableau.
Variante▲
Il est aussi possible de calculer les xi(k+1) à partir du dernier. Cela revient à permuter le rôle des matrices L et U . La formule de récurrence devient :
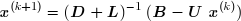
qui permet de calculer les composantes de x(k+1) lorsque celles de x sont connues :
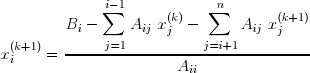
Erreur▲
A chaque itération, le vecteur trouvé x(k+1) comporte une certaine erreur :
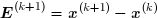
On pose P = D +L -1U . Il vient alors :
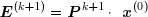
Convergence▲
L'algorithme converge si ou, ce qui revient au même, .
Théorème : une condition nécessaire et suffisante pour que 
est que les modules de toutes les valeurs propres de P soient strictement inférieures à 1.
Théorème : la formule de récurrence converge, quel que soit x(0), si la matrice A est à diagonale dominante, c'est-à-dire si la valeur absolue de chaque terme diagonal est supérieure à la somme des valeurs absolues des termes rectangles placés sur la même ligne.
Résidu▲
On appelle résidu le vecteur R (k) = B - A x (k) . La précision exigée étant donnée, on arrête les itérations lorsque :
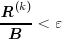
IV-C. Méthode de surrelaxation (SOR)▲
En utilisant la méthode de Gauss-Seidel, on observe qu'à chaque itération la correction apportée au vecteur solution a tendance à être sous-estimée. En d'autres termes, le vecteur converge trop lentement vers la solution. D'où l'idée d'augmenter la correction, à l'aide d'un facteur multiplicatif 
, appelé paramètre de relaxation .
Comme dans la méthode de Gauss-Seidel, on décompose la matrice A en trois matrices L , D et U :
Le système à résoudre peut alors s'écrire :
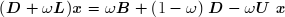
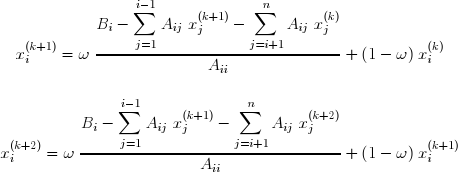
d'où l'on tire la formule de récurrence :
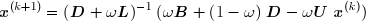
qui permet de calculer les composantes de x(k+1) lorsque celles de x sont connues :
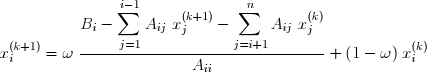
Remarque : si on pose = 1, on retrouve la méthode de Gauss-Seidel
Variante▲
Il est aussi possible de calculer les xi(k+1) à partir du dernier. Cela revient à permuter le rôle des matrices L et U . La formule de récurrence devient :
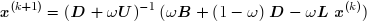
Ce qui permet de calculer les composantes de x(k+1) lorsque celles de x sont connues :
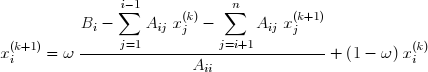
Erreur▲
A chaque itération, le vecteur trouvé x(k+1) comporte une certaine erreur :
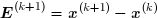
On pose P = D +L -1U . Il vient alors :
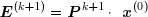
Convergence▲
L'algorithme converge si ou, ce qui revient au même, .
Théorème : une condition nécessaire et suffisante pour que est que les modules de toutes les valeurs propres de P soient strictement inférieures à 1.
Théorème : la formule de récurrence converge, quel que soit x(0), si la matrice A est à diagonale dominante, c'est-à-dire si la valeur absolue de chaque terme diagonal est supérieure à la somme des valeurs absolues des termes rectangles placés sur la même ligne.
Résidu▲
On appelle résidu le vecteur R (k) = B - A x (k) . La précision exigée étant donnée, on arrête les itérations lorsque :
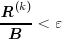
Méthode de surrelaxation symétrique (SSOR)▲
La surrelaxation successive symétrique (SSOR) est une variante qui consiste à faire jouer le même rôle aux matrices L et U , en alternant une itération dans laquelle on commence par la première composante du vecteur x et une dans laquelle on commence par la dernière. On a donc une paire de formules de récurrence :
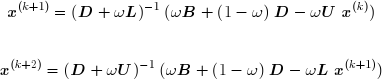
qui permettent de calculer les composantes de x(k+1) et x(k+2) lorsque celles de x sont connues :
